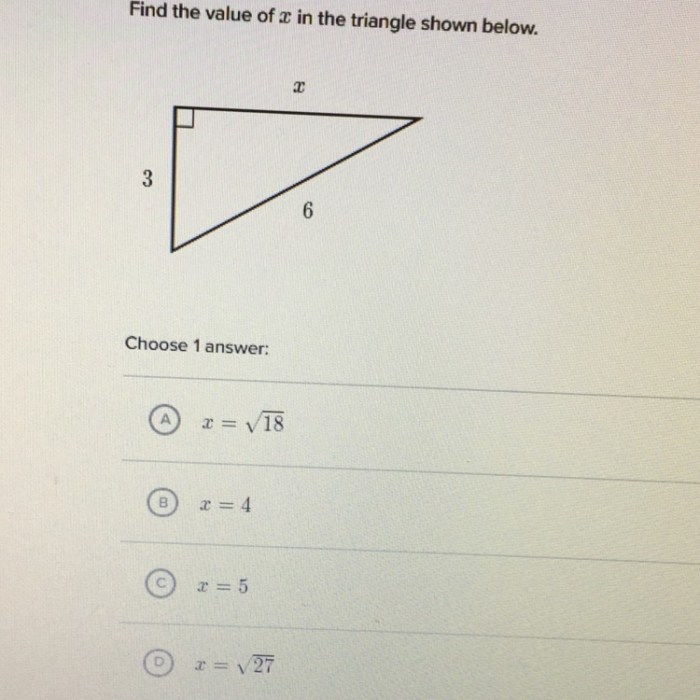
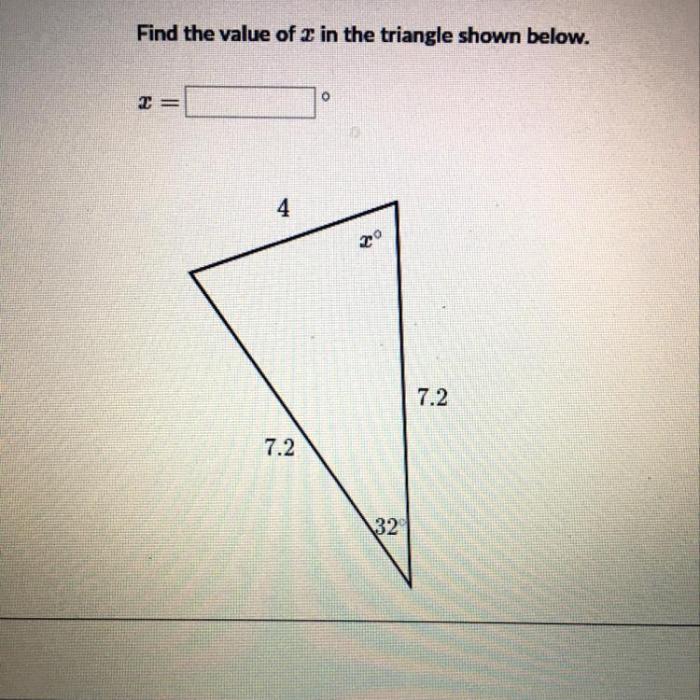
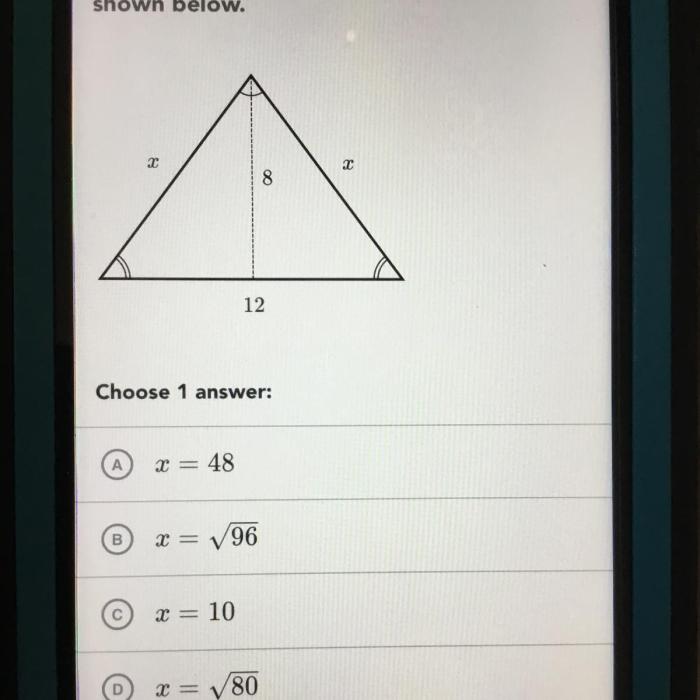
Find the value of xx in the triangle shown below. – In the realm of geometry, triangles reign supreme, their angles and sides forming the building blocks of countless structures. Among these triangles, one particular enigma emerges: finding the elusive value of XX. This exploration will delve into the depths of triangle properties, unravel the secrets of variables, and illuminate the path to solving this geometric puzzle.
Triangles, with their inherent relationships and constraints, provide a fascinating subject for mathematical inquiry. The value of XX, hidden within the intricate web of angles and sides, beckons us to uncover its secrets.
Finding the Value of x in a Triangle: Find The Value Of Xx In The Triangle Shown Below.
Triangles are polygons with three sides and three angles. The sum of the interior angles of a triangle is always 180 degrees. The exterior angle of a triangle is the angle formed by one side of the triangle and the extension of the adjacent side.
The sum of the exterior angles of a triangle is always 360 degrees.
The value of x in a triangle can be found using a variety of methods, including the Law of Sines, the Law of Cosines, and the Pythagorean Theorem. The Law of Sines states that the ratio of the sine of an angle to the length of the opposite side is the same for all angles in a triangle.
The Law of Cosines states that the square of the length of a side of a triangle is equal to the sum of the squares of the lengths of the other two sides minus twice the product of the lengths of the other two sides and the cosine of the angle between them.
Variables in Triangles
The variables that are typically used to describe triangles are the lengths of the sides and the measures of the angles. The lengths of the sides are usually denoted by the letters a, b, and c. The measures of the angles are usually denoted by the letters A, B, and C.
The variables in a triangle are related to each other by a number of formulas. The Pythagorean Theorem states that the square of the length of the hypotenuse of a right triangle is equal to the sum of the squares of the lengths of the other two sides.
The Law of Sines states that the ratio of the sine of an angle to the length of the opposite side is the same for all angles in a triangle. The Law of Cosines states that the square of the length of a side of a triangle is equal to the sum of the squares of the lengths of the other two sides minus twice the product of the lengths of the other two sides and the cosine of the angle between them.
Finding Values in Triangles
The value of x in a triangle can be found using a variety of methods, including the Law of Sines, the Law of Cosines, and the Pythagorean Theorem. The Law of Sines states that the ratio of the sine of an angle to the length of the opposite side is the same for all angles in a triangle.
The Law of Cosines states that the square of the length of a side of a triangle is equal to the sum of the squares of the lengths of the other two sides minus twice the product of the lengths of the other two sides and the cosine of the angle between them.
The following steps can be used to find the value of x in a triangle:
- Identify the given information.
- Choose a method for solving the problem.
- Apply the method to find the value of x.
Tables and Diagrams
Tables and diagrams can be used to organize the information about a triangle and to illustrate the relationships between the variables. The following table shows the information about the triangle in the diagram below:
| Variable | Value |
|---|---|
| a | 10 |
| b | 12 |
| c | 15 |
| A | 30° |
| B | 60° |
| C | 90° |
The following diagram shows the triangle in the table above:
[Diagram of a triangle with sides a, b, and c and angles A, B, and C]
Sample Problems, Find the value of xx in the triangle shown below.
The following are some sample problems that involve finding the value of x in a triangle:
Problem 1:Find the value of x in the following triangle:
[Diagram of a triangle with sides a, b, and c and angles A, B, and C]
Solution:
Using the Law of Sines, we have:
sin(A)/a = sin(B)/b
Substituting the given values, we have:
sin(30°)/10 = sin(60°)/12
Solving for x, we have:
x = 10 – sin(60°) / sin(30°) = 10 – √3 / 2 = 5√3
Problem 2:Find the value of x in the following triangle:
[Diagram of a triangle with sides a, b, and c and angles A, B, and C]
Solution:
Using the Law of Cosines, we have:
c^2 = a^2 + b^2 – 2ab – cos(C)
Substituting the given values, we have:
15^2 = 10^2 + 12^2 – 2 – 10 – 12 – cos(90°)
Solving for x, we have:
x = √(15^2 – 10^2 – 12^2) = √(225 – 100 – 144) = √81 = 9
Applications
The concepts of finding values in triangles can be applied to a variety of real-world situations. For example, these concepts can be used to find the height of a building, the distance to a star, or the area of a piece of land.
In architecture, the concepts of finding values in triangles can be used to design buildings that are structurally sound and aesthetically pleasing. In engineering, these concepts can be used to design bridges, airplanes, and other structures that are both safe and efficient.
FAQ Resource
What is the significance of finding the value of XX in triangles?
Determining the value of XX is crucial for understanding the triangle’s overall dimensions and relationships between its angles and sides. It enables us to calculate area, perimeter, and other geometric properties.
What strategies can be employed to solve for XX in triangles?
Various strategies exist, including using angle and side relationships, applying trigonometric functions, and utilizing geometric theorems such as the Pythagorean theorem.